A new tool for the hydrometric toolbox: monitoring river discharge from space

The hydrometric toolbox

The hydrometric toolbox comprises a set of methodologies to determine streamflow in a river. It includes a collection of different techniques such as measurement weirs, rating curves in combination with water level monitoring, the deployment of permanent ADCPs, optical methods to monitor surface velocity, and emerging satellite-based technologies that employ deep learning.

Each tool has its own application area. The selection of the appropriate tool is a function of multiple parameters that include the hydraulic conditions, location, site access, site security, monitoring objectives (i.e. the end use of the discharge data), the available budget and manpower, the need for defensible data, etc.

Keeping costs low is imperative. Water resources agencies typically have a restricted budget and field visits and sophisticated instruments—such as permanent ADCPs—are expensive. Consequently, in many countries the number of in-situ river stations measuring discharge is steadily decreasing.

It explains the appeal of AI and satellite-based river monitoring techniques. These emerging technologies promise an affordable solution to improve water data availability in ungauged and remote basins while keeping costs low. But can they live up to these expectations on closer inspection?

This post will examine the potential utility of a new tool in the hydrometric toolbox: monitoring river discharge from space.

Monitoring river discharge from space

Daniel Scherer et al published a paper “Monitoring river discharge from space: An optimization approach with uncertainty quantification for small ungauged rivers” in Remote Sensing of Environment (2024).

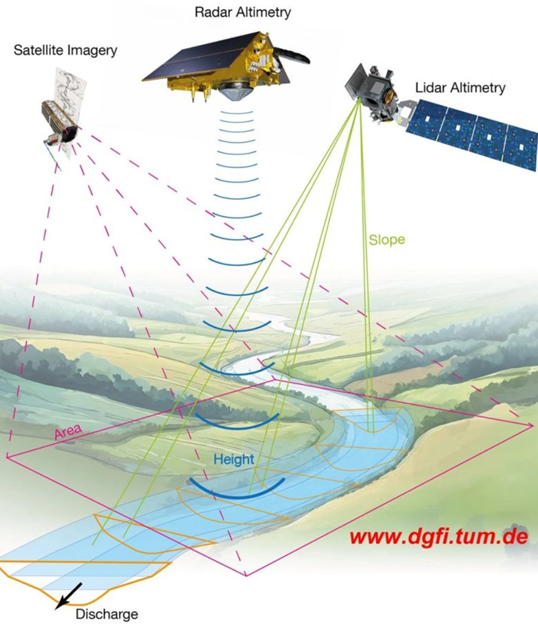
The approach uses high-resolution satellite altimetry to measure the longitudinal slope and the cross-sectional profile of the river. Note that only the portion above minimum water level can be measured. The unobserved part of the cross section—i.e. the part below minimum water level—is first estimated with a depth function and subsequently adjusted in an optimization process.

The methodology employs the principle of mass conservation—which considers discharge to be constant in a short river reach in a short period of time—to approximate the unknow roughness coefficient and the unknow part of the cross section. This is accomplished by identifying many measurement sites on a single river reach and subsequently applying an optimization function based on the assumption that discharge in all cross-sections should be equal (i.e. the principle of mass conservation—provided there is no water offtake or tributary inflow on this reach). Hence the approach effectively transforms measuring discharge into solving a large optimization problem. Deep learning AI technology is very good at this.

Thus, the methodology is promising in principle.

The hydraulic conditions

The approach is based on the following assumptions:

1. ‘Open-channel flow’, where gravity is the only driving force for flow; this is a valid assumption; it implies that flow is a function of 1) slope, 2) channel roughness, and 3) the cross section; the latter is characterized by the hydraulic radius R.
2. ‘Pressure head’ is the dominant term in the energy equation, which is valid for sub-critical flow conditions; this is a valid assumption for the selected measurement sites.
3. Steady state, which means that the discharge in all cross-sections is equal; this is a realistic assumption for most rivers for the time step used in this methodology.
4. Uniform-flow or gradually varied flow; it implies that shape, roughness, and slope is constant over the length of the channel sections that serve as the hydraulic controls for the respective cross-sections that represent a measurement site; this assumption is probably not valid; nevertheless, it can be addressed by adjusting the roughness coefficient; this is a common practice in hydrometry. It does, however, complicate the optimization process because it increases the degrees of freedom.
5. There is a unique relation between stage and discharge; this is a valid assumption since the measurement sections have been selected with this condition in mind.
6. The cross-section below baseflow has a regular parabolical shape and follows the empirical width-to-depth relationship derived from observations by Moody and Troutman (2002); this assumption is not true in practice; cross sections are typically irregular.

The below figure presents a typical ADCP measurement. It concerns River Luipa at Mbingu—in the Kilombero basin in Tanzania—on 25 April 2017. While flow is quite regular, it is not uniform and confirms that assumption 4) is not valid in this case. In addition, note that the shape of the cross section is not parabolic.

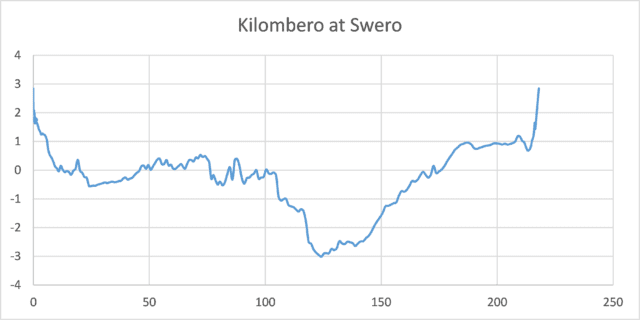
The picture and cross-section depicted below are from river Kilombero at Swero. It is a majestic permanent river that—at first glance—seems representative of a river with stable and regular hydraulic conditions. The cross-section, however, is not a parabola. In fact, it is rather irregular with a distinct deep channel. Hence this cross-section implies that assumption 6) is also not valid.

Satellite discharge monitoring: the application domain

As discussed above, discharge in open channels is a function of 1) slope, 2) channel roughness, and 3) cross-section. The satellite-based methodology measures—with some precision—1.5 out of these 3 variables: the slope and part of the cross-section. However, the approach does not measure channel roughness and that part of the cross-section that is below minimum flow level. These unknown variables are determined through an optimization process. Yet at least one assumption at the basis of this optimization process—the parabolic shape of the cross-section—is not always valid. In fact, of all the hydraulic controls that I reviewed in the last few years (>100), a large segment—I would say more than 50%—are quite irregular and not (at all) parabolic in shape. In those instances, the shape of the cross section is primarily dictated by local geologic features. Hence river morphology in these cases does not adhere to empirical width-to-depth relationships that are based on a long-term equilibrium between the hydrologic regime and the sediment regime. Note that when local geology determines the shape of the cross section, river characteristics (such as roughness and flow conditions) can change quite suddenly from one location to the next.

The optimization approach will probably not work for these conditions. There are simply too many degrees of freedom.

In the study by Scherer et al, the minimum number of cross-sections used for the optimization exercise was 5 (table 1; for rivers Kuran and Oueme) while most rivers required far more (up to 29). Further, there was no correlation between the number of cross-sections and the measurement uncertainty. This implies that the optimization process is not yet consolidated and fully developed.

Thus, the application of satellite-based technology for discharge measurement has not yet matured. It seems contingent on some level or regularity—along the longitudinal course of the river—of the cross section, channel roughness, and flow conditions. These conditions are probably mostly met in wide alluvial plains in the lower reach of a river, provided there is still some slope and river braiding does not yet occur.

Defensible water data

Water data are defensible when you can prove that each record is reliable and correct. It is based on a transparent process for each step in the data acquisition process. For the satellite-based technique, the current approach to optimize the cross-section and channel roughness is not yet fully controlled and still resembles a ‘black box’ routine. The satellite-based methodology, therefore, does not produce defensible water data.

In addition, the requirement of less than 10% measurement uncertainty could only be met for 7 out of 27 studied rivers. Measurement uncertainty varied widely and was between 6% and 34%. Worse, the measurement uncertainty could not be predicted, which further suggests that the process is not yet fully consolidated. Note that an ADCP discharge measurement is only approved when 4 consecutive measurements are within a 5% range. This points to a different level of data accuracy between in-situ discharge measurements and satellite observations.

Thus, while the method certainly has promise, it does not yet produce data that can be used for effective water resources assessment and operational management. It also does not yet produce defensible data.

Closing comments

The hydrometric toolbox: from satellite monitoring to rating curves to citizen science, and everything in between

The satellite-based river monitoring technique discussed in this post is a welcome addition to the hydrometric toolbox. Nevertheless, the methodology is still under development and its application domain is limited up to now. Specifically, the wide range in measurement uncertainty precludes the use of the technique for practical assessments and operational purposes.

To reduce the degrees of freedom in the optimization process, one could consider combining the methodology with a few in-situ ADCP measurements. This should not be expensive. It would greatly reduce the range of the potential boundary conditions and thus simplify the optimization process. It would also make the data somewhat defensible. My sense is that such a hybrid approach could be operational within a short period of time. It’s worth looking at!

---

REFERENCES

Scherer D. et al, Monitoring river discharge from space: An optimization approach with uncertainty quantification for small ungauged rivers, Remote Sensing of Environment 315 (2024) 114434, Elsevier 2024

---